Optimal Transport in Large-Scale Machine Learning Applications

Introduction: Optimal transport, especially Wasserstein distance, has been a popular tool in machine learning applications in the recent years. Despite its appealing performance, Wasserstein distance has been known to suffer from high computational complexity, namely, its computational complexity is O(m3 log m) when the probability measures have at most m supports. In addition, Wasserstein distance also suffers from the curse of dimensionality, namely, its sample complexity is at the order of O(n-1/d) where n is the sample size. A well-known solution to these problems is sliced Wasserstein (SW) distance, which has computational complexity O(m log2 m) and sample complexity O(n-1/2).
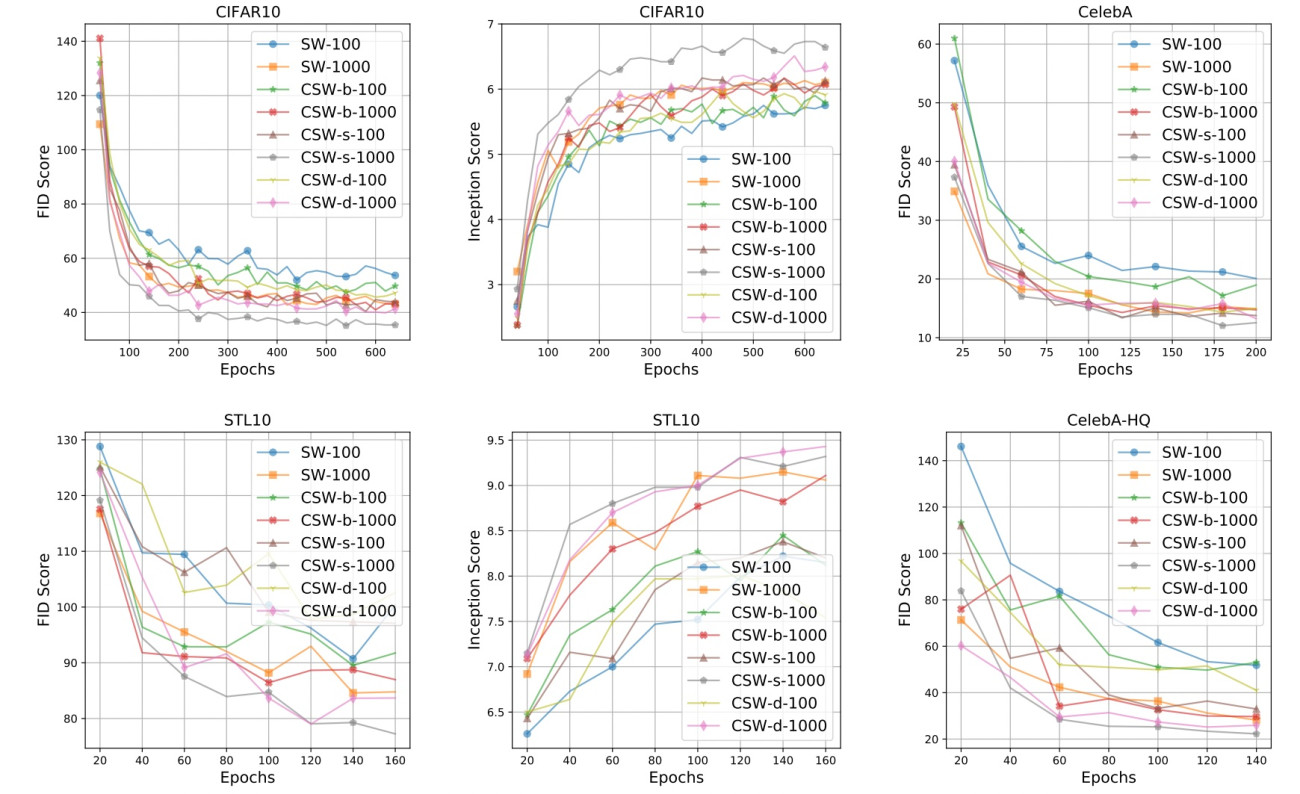
Convolutional Sliced Wasserstein: Despite being applied widely, the conventional formulation of sliced Wasserstein is not well-defined to the nature of images. In particular, an image is not a vector but is a tensor. Therefore, a probability measure over images should be defined over the space of tensors instead of vectors. The conventional formulation leads to an extra step in using the sliced Wasserstein on the domain of images which is vectorization. This extra step does not keep the spatial structures of the supports, which are crucial information of images. Furthermore, the vectorization step also poses certain challenges to design efficient ways of projecting (slicing) samples to one dimension based on prior knowledge about the domain of samples. To address these issues of the sliced Wasserstein over images, we propose to replace the conventional formulation of the sliced Wasserstein with a new formulation that is defined on the space of probability measures over tensors. Moreover, we also propose a novel slicing process by changing the conventional matrix multiplication to the convolution operators. As a result, we obtain a efficient family of sliced Wasserstein variants which is named convolutional sliced Wasserstein (CSW) [2]. Comparing CSW to SW in generative modeling, we observe that CSW performs better than SW while CSW consumes less memory than SW.
Amortized Sliced Wasserstein: To improve further the performance of sliced Wasserstein generative model, we propose to apply amortized optimization for seeking the most informative projecting direction in each pair of mini-batch measures. By using amortized optimization, we can avoid an iterative optimization procedure in each pair of mini-batch measures to find the projecting direction that can maximize the projected distance. We formulate the approach into amortized sliced Wasserstein (ASW) [1] losses and propose some forms of amortized models including linear model, generalized linear model, and non-linear model. We show that ASW yields a better quantitative scores than mini-batch sliced Wasserstein and mini-batch max sliced Wasserstein (Max-SW). Furthermore, ASW can be computed in less time than SW and Max-SW.

References
[1] Khai Nguyen and Nhat Ho. Amortized projection optimization for sliced Wasserstein generative models. Advances in Neural Information Processing Systems (NeurIPS), 2022.
[2] Khai Nguyen and Nhat Ho. Revisiting sliced Wasserstein on images: From vectorization to convolution. Advances in Neural Information Processing Systems (NeurIPS), 2022.
Expenditure: The report is part of the project ”On the computational and methodological perspectives of optimal transport in machine learning”, which is supported by the IFML grant. The first-year PhD student, Khai Nguyen, has been involved in this project and finished two papers that were recently accepted at Advances in NeurIPS, 2022 (cf. the papers [1] and [2]). The money of this project was used to support Khai’s stipend in Fall 2022, Khai’s expenses when he traveled to ICML 2022, and the summer salary of the PI, Nhat Ho, in 2022.